by WWM | Mar 16, 2017 | Investor Profile, Risk
In Standard Deviation Limitations, I noted that one potential weakness is human behavioural characteristics.
The risk tolerance of each individual is different. It is based on one’s experiences, desires, needs, objectives, and attitudes.
Understanding a person’s unique risk tolerance is critical. How investors view the risk and associated expected return of investments will guide their investment strategy. Everyone differs to some extent.
Today we will look at few questions that shape an individual’s perception of risk.
Consider how you perceive risk as we go through these questions?
Is risk the losing of invested capital?
For many, the thought of losing money is their greatest fear.
These investors typically consider the risk of losing money in absolute dollar terms as compared to the original cost of the asset. Some investors feel that money is only “lost” when the investment is actually sold. Others feel the pain even for losses that are not yet realized.
When we looked at risk, we saw that the greater the investment risk (i.e., standard deviation), the greater the volatility of the investment. That is, the greater the probability that the actual return would deviate from the expected return.
If you fear losing money, you might be more comfortable investing in extremely low risk assets. Sacrifice potentially higher returns for certainty, as well as minimizing the risk of actually incurring an absolute loss.
Is risk the unfamiliar?
Individuals often fear the unknown.
For investors, investments with which one has little or no knowledge of, or appear to be complex in nature, may be seen as riskier.
A good example is the writing of covered call options. Many investors have no experience dealing with options. The mechanics and even the terminology may be intimidating. If I suggested that they incorporate covered calls in their investment portfolio, most investors would be hesitant. Their uncertainty is internalized as increasing the investment risk.
But that is simply the perception. The reality is that covered call options can be an excellent tool within one’s portfolio. While not something I might recommend initially for investors, as investment knowledge and experience improves, one can see that certain options strategies are not risky nor overly complex to execute.
While it is fine to be cautious with unfamiliar investments, that does not necessarily mean they are more risky. Take a little time to learn about areas where you have no knowledge. You might find that the investment is not as risky, nor intimidating, as your initially thought.
Is risk being once bitten twice shy?
Individuals often view investments on which they have previously lost money as unattractive or riskier than they really are.
For example, you purchased 10 ounces of gold in 2012 at USD 1600 per ounce. The investment fell over time and you sold in 2015 for USD 1100 per ounce.
In 2017, you read that gold is recommended as a great mid to long term investment. Based on your prior experience losing money on gold, there is a strong probability you will find this new recommendation unattractive or high risk.
However, that unattractiveness or increased risk is merely a perception and not reality. Whether you gained or lost money on a specific investment in the past has no connection with how well you will do in the future.
Of course, I also meet investors who like to jump back in on investments they previously lost money on. Payback, they are due, karma, pick your reasoning.
Is risk not following the crowd?
Following the conventional wisdom and expert recommendations is usually comforting.
It is always good to find that others, especially experts, agree with your investing decisions. Or that your decisions are based on the consensus of many who may be “smarter” than you. If you lose on the investment, you can take some solace knowing that many others did so as well.
Taking contrary investment positions is more stressful to many individuals. Going against the tide may be seen as a risky proposition. After all, who are you to know more than everyone else?
For example, if the “talking heads” on the business channels are all recommending avoiding Canadian natural resource equities, it takes a bit of nerve to go out and buy shares in these companies.
Given the track record of many “experts”, I am not sure following their advice is often wise.
Investment bubbles are often the end result of following the crowd and engaging in “herd mentality”.
Is risk historically based?
Finally, investors often focus on the past when assessing risk.
Individuals consider historic returns when extrapolating into the future. While history can be a predictor of the future, it is the expected returns (and associated risk) that is more important.
Situations change, both good and bad, and that can impact the risk of an investment.
Consider a mutual fund whose mandate is shares in mining companies. Performance over the last 10 years averaged 15% and risk standard deviation was 4%. Well ahead of other funds in the same category. Based on past results you invest.
However, six months ago the fund decided to sell its investments in traditional mining companies and focus on higher risk companies in Africa and South America. Specifically, countries with less stable companies, young free-market economies, and inefficient markets. Unhappy with the shift in strategy, the successful management team quit. To save money, the fund company has the managers of their banking mutual fund take over management of the mining fund.
Although historic risk was 4%, these recent factors will significantly increase risk levels in the near future.
Data comforts investors in their decision making. And it should. But if you rely too much on the past, you might err in the future. Historic statistics are only applicable if the circumstances in which they occurred are still relevant going forward.
That is why in every mutual fund prospectus you will see “past performance is no indicator of future results.” Or similar.
How did you respond to these questions?
The answers will help you arrive at your personal risk tolerance level. This will guide you as to investments you are comfortable to invest your capital in.
Do you fear the risk of a real loss? Or do you take (hopefully, calculated and prudent) risks to attain potentially higher returns?
Do you avoid the unfamiliar? Or are you an adventurer who seeks out new investment ideas?
Does a prior loss in an asset class or investment cause you to shun them in future? Or is it a chance for revenge?
Do you get comfort relying on experts and the consensus or do you prefer going against the flow?
There are no “right” answers. How you see risk is based on your life history.
However, while risk tolerance levels are unique to each person, I would like to influence each of you to some extent.
I cannot do much about your personality, life experiences, investment objectives, personal constraints, etc. And how they all impact your risk tolerance.
However, I hope to show you that it is best to take a view of risk with as little emotional involvement as possible. That by improving your base investment knowledge and learning what questions to ask, you can become more objective in your decision making.
I fully realize that this is a challenge for almost all individual. But if you can develop a more disciplined approach to investing, you will be in better position to succeed over the long run.
by WWM | Mar 10, 2017 | Risk
While standard deviation is indeed very useful in assessing investment risk, there are limitations to its use.
In analyzing any investment, smart investors factor in these potential weaknesses, including: asymmetric payoffs; historic versus future results; the need for context; human behavioural traits.
Awareness of these potential pitfalls will help you better incorporate standard deviation calculations in your own analysis.
Asymmetric Payoffs
In our previous discussion, we used examples with normal distributions. There was a reason for that. Standard deviations are poor tools for investments with asymmetric payoff profiles.
In a normal distribution, the payoff profile is symmetric. The normal distribution curve should look the same on both sides of the mean. Results should be equally disbursed around the middle. The tails on each end of the curve are symmetric. That is why one can use multiples of the standard deviation (e.g. 2 standard deviations from the mean contains 95% of all potential results) to determine outcome probabilities.
In an asymmetric profile, the distribution curve is skewed on one side of the mean or the other. By skewed, I mean that the tails are unequal in the distribution outcomes.
If the left side tail is more pronounced, there are more actual results to the right side of the mean. But a relatively few extremely small valued outliers drag the tail of the curve leftward. This is being “negatively skewed”.
If the right side of the curve is longer, there are more results on the left side of the mean. But a relatively small number of extremely high value outliers push the tail to the right. In this case, the distribution would be “positively skewed”.
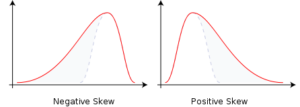
It is easy to see why skewed distributions limit the usefulness of the standard deviation as a risk measurement. In the graphs above, say the mean is 10 and the standard deviation is 2. Under a normal distribution, 68% of results should lie between 8 and 12. 95% of outcomes between 6 and 14. But, as you can see in these two graphs, the distribution pattern is not symmetric. So it is unlikely that the results will fall in the range as intended for standard deviation to be helpful in analyzing the investment.
In the real world, positively skewed distributions are more common than negative ones.
A Real-Life Example of Skewed Distributions
Employee compensation is a typical example. You have 100 people in a company and the average, or mean, salary is $50,000. Of the 100 staff, most likely earn close to that $50,000. Some will make less than the average. But even the most junior staff will earn a minimum level, perhaps $10,000 to $20,000. That is the tail on the left side of the curve.
If compensation was normally distributed one would expect senior management to receive approximately $80,000 to $90,000. A similar “distance” from the mean as the lower junior staff. That creates a nice symmetric, bell shaped curve.
In reality, the President and direct subordinates may earn substantially more. In this example, say the President earns $325,000 and the three Vice-Presidents earn $225,000 each.
Senior management is very few in number, but they distort the distribution curve in two ways.
One, total compensation is $5 million (100 staff averaging $50,000 each), yet only 4% of all employees earn 20% of the compensation (4 senior staff make $1 million combined). That inflates the overall mean relative to the typical employee.
If you eliminated those 4 from the calculation, there would be 96 staff earning $4 million. This results in an adjusted mean of only $41,667 for non-senior management employees. Probably a more realistic figure to compare employee averages. Most staff will earn closer to this average.
Two, the very small number of extremely high value earnings will lie on the far right side of the distribution. These salaries push the curve much farther to the right than if all compensation was normally distributed. The average will be further right than the peak of the curve. This results in the long right-hand tail and the positive skewing of the distribution.
You can likely think of many more examples of where outcomes are not symmetric in reality.
In the realm of investing, option strategies and portfolio insurance are examples of asymmetric payoff profiles.
Not areas we shall delve too deeply. However, I wanted to properly explain asymmetric distributions to further reinforce the understanding of normal distributions.
The Past is Not the Future
A second issue with standard deviations is their use of historic data. Past results might be a predictor of the future, but results may also change over time.
New management, different product lines, increased competition, expiration of patents, etc., all may impact future results and therefore alter the standard deviation.
Be careful in placing too much faith in historic results.
Standard Deviations Need a Context
Standard deviations should never be considered on their own. One needs to factor in the expected return as well.
For example, investment A has a standard deviation of 6%. Investment B has a standard deviation of 10%. If you only look at the standard deviation, B is the riskier investment.
But what if I also tell you that the expected return for A is 4% and 15% for B?
At a 95% confidence interval below the expected return, you could actually lose more with investment A than B. Without getting into the calculations, you could lose 5.9% with A and only lose 1.5% with B.
To address this issue, you need to consider the concept of “Value at Risk”. We may or may not get into this slightly more complex topic at a later date. But no promises or threats.
Human Behaviour
Standard deviations are unable to quantify behavioural aspects of investing risk.
We will devote some time to Behavioural Risk issues at a later date. In essence, it looks at how human behaviour affects the investing decision-making process .
It is an interesting and important topic. And it will not put you to sleep.
So there is a quick overview on the limitations of standard deviations as a risk measure.
You will not need to calculate means or standard deviations. But it is important to know what they are and why they are useful. Then, when you do encounter them, you understand the value and limitations of both measurements.
by WWM | Mar 3, 2017 | Risk
Let’s continue our look at Investment Risk in Detail.
In the last post, we ended with an example. Two investments with the same 5% annual expected return. “A” had a stable return history, so the probability of earning the 5% next year is high. However, “B” had a highly volatile return history, so the probability of earning exactly 5% next year is low.
Same expected annual return over time, but much different likelihoods of actually earning the 5% return in any one year.
As an investor, how does one differentiate between the two investments?
A very important question. Hint: it may involve investment risk.
Standard Deviation
In comparing two investments with the same expected return, it is extremely useful to quantify the investment risk.
And remember, investment risk is simply the volatility of an asset. High certainty of future returns as expected, low risk. Wide fluctuations in returns versus expected, high risk.
To be of any practical use, a measure of risk must have a definitive value that may be analyzed by investors. Standard deviation is the statistical measurement of the movement of returns around the mean.
In investing terms, the standard deviation is the measure of the total risk of the investment.
Under a normal distribution, the majority of actual returns will occur relatively close to the mean or expected return. This is good for predicting future results.
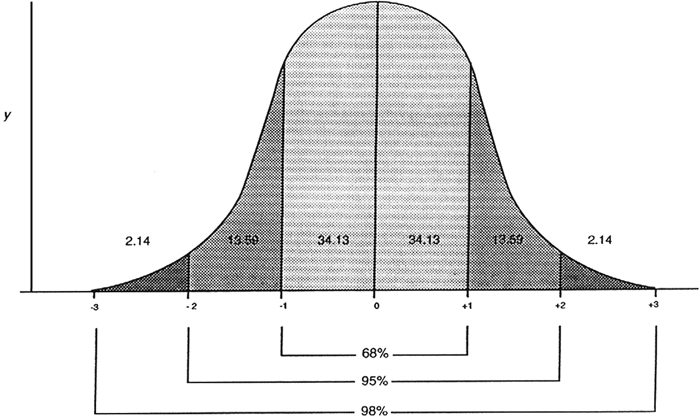
In a normal distribution, 68% of all returns will fall within 1 standard deviation of the mean. 95% of all returns will take place within 2 standard deviations of the mean. 98% of all returns will occur within 3 standard deviations of the mean.
Say the mean is 10 and standard deviation is 3. As 68% of results occur within 1 standard deviation from the mean, that equates to between 7 and 13. While 95% of the time, results will lie within 2 standard deviations. So, between 4 and 16.
This is consistent in any normal distribution.
Nice to know the range of possible results with 95% confidence. Makes investment analysis easier.
If you are concerned about negative returns, in a normal distribution, there is only a 2.5% probability that the next year’s actual return will be lower than 2 standard deviations from the mean. That is good to know.
Note that there is a 95% probability that a return will fall within 2 standard deviations of the mean. So there is a 2.5% probability that next year’s return will exceed 2 standard deviations (i.e. the far right tail of the curve) and a 2.5% chance that the return will be below 2 standard deviations from the mean.
Theory, theory, theory. Let us look at how this applies to real world investing.
An Example of Standard Deviation
Perhaps you have two investment choices. “A” offers an expected return of 10% over a one year period. “B” offers an expected return of 13% over the same period.
Ceteris paribus (all else equal), “B” should be your choice as it offers a higher expected return than “A”.
But all else is never equal, except in Latin phrases.
You notice during your research that each investment has a standard deviation assigned to it. “A” has a standard deviation of 2. “B” has a standard deviation of 9. You also note that both investments have normal distributions.
So how can standard deviations help your investment decision?
Remember that 68% of the time, actual returns will lie within 1 standard deviation of the expected return and within 2 standard deviations 95% of the time.
“A” has an expected return of 10% and a standard deviation of 2. That means 68% of all possible returns actually achieved will be between 8% and 12%. And that 95% of the time you will experience returns between 6% and 14%.
A fairly stable distribution of returns over time. Not a volatile asset, “A” has a relatively low standard distribution.
For investors worried about experiencing a loss or lower than desired returns, 95% of the time they will, at worst, earn a 6% return. Nice to know if you are worried about absolute losses.
“B” has an expected return of 13% but a standard deviation of 9. 68% of results will lie between 4% and 22%. And 95% of the returns will be between -5% and 31%.
“B” is much more volatile in its returns than “A”. This is reflected by the higher standard deviation value.
Very nice upside potential of 31% return. But if concerned about lower potential returns or even losses, “B” might be too risky with it’s potential -5% return.
Armed with this new standard deviation information, does your investment decision change?
It might, it might not.
Investment Risk is a Relative Concept
As we discussed previously, the concept of risk is different for every individual.
Risk is therefore a relative term, not an absolute.
Some investors want to limit their downside investment risk and any possibility of experiencing a loss. Widows and orphans are in this group. As are many other investors.
These individuals willingly accept a lower expected return in exchange for a greater certainty of that return being realized. Investments whose potential returns are less volatile or variable are desired. A less risky result is preferable to higher potential returns (and more downside risk).
Other investors might be lured by the potentially high returns of “B”. Option “A” should rise no higher than 14% (97.5% of the time), whereas “B” could beat that return easily (of course, it could also do significantly worse as well).
Risk Aversion Versus Risk Seeking
While each investor takes a different view of risk, most investors (as opposed to speculators, who we will discuss later) tend to be risk averse. That is, when faced with two investment choices of similar return, they select the less risky one.
In contrast, risk seekers will actively assume greater levels of risk in the hopes of achieving higher returns. Their risk tolerance is significantly higher than risk avoiders.
In the capital markets, you need some investors to be risk seekers and others to be risk avoiders. The system will not properly function if everyone is the same. As we will see later, hedgers actively attempt to reduce their risk exposure. But they need to transfer that risk somewhere. Without risk seekers, there would be no one to assume the hedger’s risk and the markets would be very inefficient.
In the example above, I would suggest “A” is the better choice based solely on the information given. I say that because the relatively greater expected return of “B” is not large enough to warrant the significantly higher level of risk you must assume. So while I have no problem with risk seekers as an investor class, risk should be assumed prudently.
A Rule to Remember
“When faced with two investments offering identical expected returns, investors will always choose the one with less risk.”
Or stated another way:
“When faced with two investments having identical risk, investors will always choose the one with the higher return.”
Of course, the issue is choosing between two investments when they have different expected returns and standard deviations. A more likely scenario in the real world. And the choice usually comes down to the individual investor’s risk tolerance and unique personal circumstances.
In the near future we will look at the risk-return relationship and the implications of risk aversion and risk seeking on investment decisions. After which, please revisit this example and see if your original opinion has changed at all.
Regardless of your personal risk profile, the standard deviation of an investment is a very useful piece of information to have at hand. But be aware that there are limitations to the use of standard deviations.
We will look at these limitations in my next post.
by WWM | Feb 24, 2017 | Risk
Today we begin to look at investment risk in greater detail.
This expands on our preliminary discussion in Defining Investment Risk.
Investment Risk Revisited
Previously we defined investment risk as a speculative risk. As such, investment risks provide the possibility of incurring a loss, breaking even, or profiting. This differs from pure risks where you cannot profit from the risk.
I wrote that investment risk is the probability that the actual returns on an investment will differ from the expected returns. The higher the probability of a different result, the greater the risk. The lower the probability of a different result (or the greater the certainty of the same result), the lower the risk.
That may mean a loss like with a pure risk. A gain, but less than was expected. Or it could mean a bigger return than anticipated. So a risk, yes. But one that may bring rewards.
Investment risk is simply the level of volatility of returns. Not a risk of loss. Important to remember.
Investment Risk in a Graph
For those of you poor souls who have taken statistics courses, investment risk is typically viewed from a normal distribution perspective. The graph below is an example of a normal distribution curve.
Not the easiest concept to explain in a blog post (augmented by the fact that I am not a statistics professor), so we shall try and keep this basic.
Outside of a few key concepts, I intend to keep the statistics and formulae at a minimum. Not fun to read, nor usually necessary to understand the principles. But I think it worthwhile for risk as it is calculated via standard deviations.
Like head-ache medication though, I caution you not to read this post while driving or operating heavy equipment. The following may just put you to sleep.
Normal Distribution
You may also recognize the graph above as a Bell curve, so named for its shape. Or you may have heard it called a Gaussian distribution; named after Carl Friedrich Gauss.
Within a normal distribution, historic outcomes are placed on the graph and a distribution similar to the one above typically results.
The “Y” axis represents the actual outcomes. The more results at a certain level, the higher the curve. The bottom “X” axis represents the distance from the average (i.e. mean) result.
It is called normal because the outcomes are symmetric in nature. You can see this by the equal spread of outcomes on both sides of the curve. Note how the tails on both the left and right sides of the curve are similar in distribution.
If the distribution was not normal, but rather skewed, one end of the curve would be longer and more pronounced than the other end.
The important thing to note with a normal distribution is the way the Bell curve looks. Most of the actual results cluster relatively close to the middle of graph. The higher the curve, the more results are at that level. As you move farther from the middle, the number of results decreases. This creates the diminishing tails at either end.
In the real world, normal distributions are common. For example, the average height of US men is 5’10”. Most American men are roughly this height. The proportion taller or shorter will continue to diminish as you move away from this average.
And it should make sense that the larger the sample size, the more appropriate the results. If you sample 3 men, you may not find an average of 5’10”. If you sample 300,000, you will get a realistic average. The same holds true with investing. The smaller the sample size or time period, the more questionable the result.
Mean
In investing, the mean is the expected return on the investment. This is represented by the average result on the above normal distribution curve, located at position 0.
The expected return may be calculated based on historical data, theoretical probability models, experience, and professional judgement. Perhaps the expected return will be 2%, 12%, 22%, etc. The 0 midpoint on the Bell curve simply represents the consensus expected return.
As most investments carry risk, actual results may differ from expected outcomes. Actual results usually lie somewhere to the left or right of the expected return. That said, there is no reason that they cannot fall exactly on the mean.
Note that you may encounter “median” as an average. It is not. A median return is one that simply takes all values, sorts them in ascending order, and determines the middle value. For example, you have 5 returns. 3, 4, 5, 16, 22. Median just puts the numbers in order and finds the midpoint. In this example, 5. There are 2 outcomes to the left, 2 to the right.
Calculating the arithmetic mean, you add up all the values and divide by the number of outcomes. In this example, the arithmetic mean is 10. Significantly different than the median.
And no, do not use median to assess investments. Median has some value, but use mean if possible.
Note that arithmetic means often have their own flaws. We will explore those and the use of geometric means later.
Investment Risk
So we know that the expected return of an investment is the mean, or average, in a normal distribution. We also know that the actual results will fall on either side of the mean.
But what does that tell us about the investment risk?
The investment risk is the variability of the actual returns around the mean. In English, simply how far away from the average return is the actual result. The average is 0, the high point on curve.
As you can see above, actual results may be both greater or less than the expected return. So investment risk applies to the possibility of higher than expected returns, not simply lower than expected ones. However, investors are usually more concerned with results to the left of the curve. That is, where the actual performance is less than the expected returns.
The risk of an investment is determined by the variability, also known as volatility, of the actual returns around the expected return. Volatility is the amount of fluctuation in the actual returns from the expected returns. The greater the degree of volatility, the greater the risk of the investment.
The tighter the probability distribution of the expected future returns around the mean, the greater the certainty of the returns. As the certainty of the return increases (i.e. the less potential difference between the actual and expected result), the smaller the amount of uncertainty or risk. In a normal distribution curve, the vast majority of actual results would amass extremely close to the mean. The bell would be quite high and narrow in width.
For results with high variability, the actual returns would be disbursed much farther from the mean. This would cause the bell shape to be shorter in height and much wider in width.
An Example of Investment Risk
For example, investment “A” has an expected return of 5% and the actual returns over the last 6 years were 4%, 6%, 5%, 5%, 6%, 4%. The distribution around the 5% mean is quite tight. You would be right to expect the return over the next year to be close to the expected outcome. The risk that the return will not be close to 5% is low.
Investment “B” also has an expected return of 5%. However, its performance for the last 6 years was 2%, 12%, -4%, 15%, -3%, 8%. The actual results are significantly different from the expected result. You should be concerned that the actual result for the upcoming year will not be close to the expected return of 5%.
Here you have two investments with the same expected return. Yet the certainty of earning 5% on A is pretty high for next year while there is very little guarantee as to what B returns. It may be 5%. Or it may be significantly different than 5%. Even experiencing a loss. A’s expected future return is pretty certain. B’s expected return will be very volatile.
That is investment risk.
So how does one differentiate between the two investments?
by WWM | Feb 20, 2017 | Risk
What is investment risk?
Investment risk is a form of speculative risk. Speculative risks differ from pure risks in that with a speculative risk there is a possibility of gain, not just loss or no change in status.
But what does that mean?
Is Investing a Gamble?
Gambling, like investing, is a speculative risk.
Perhaps you play poker with friends monthly. Sometimes you lose, occasionally you win, and a few times you may break even. But when the evening begins you do not know what the outcome will be.
Some authors claim the opposite is also true. That speculative risks are merely gambles. By extension, investing then must also be a gamble.
I do not agree with that viewpoint. Here are a couple of reasons why.
Beating the Odds
First, when visiting Las Vegas, there are steps that can be taken to improve your probability of success. You can study effective gambling strategies; avoid alcohol, emotional swings and sleep deprivation; only play games with the best odds.
However, there is a reason that Las Vegas is profitable. The odds are always in the house’s favour. In the short run one may profit. But over the long haul the probability of loss is certain for gamblers.
You can also improve your probability of success in investing. Education and experience will help you become a better investor. Taking a disciplined approach that eschews emotion from decision-making (or as Alan Greenspan would say, avoiding “irrational exuberance”) will also improve your chance of success. You may decide to only invest in assets with the “best odds” as well.
Despite media stories, the markets are not a casino. Investments are not games of chance that were expressly created to provide the casino with a built in advantage. Learning to properly invest is not simple, but it is possible to “beat the house” over the long run.
Potential Certainty of Returns
Secondly, when you enter the casino with $1000 you have no idea what you will leave with at night’s end. Depending on your luck and skill, you could win $1 million, break-even, or (more likely) go home with nothing except a few free drinks and a shrimp cocktail for your efforts. And that is not factoring in a possible trip or two to the conveniently located Automated Teller Machines.
Again, investing is different. I can list numerous investments where the outcome is known with (almost) 100% certainty. If you invest $1000 in a 1 year 5% Guaranteed Investment Certificate offered by your bank, at the end of the term you will receive $1050. Or you could invest $975.90 in a 6 month US Treasury Bill (T-Bill) yielding 5% and be confident of receiving $1000 upon maturity. Unless your bank or the US government defaults on their debts, your investment is completely safe.
While it is fair to say that investment risk is not gambling type risk, what is it then?
Investment Risk Differs Between Individuals
Investment risk is difficult to pin down. It is a concept that differs from individual to individual. What I think is risky may not be to someone else. And vice-versa. One’s personality, experiences, and personal circumstances all contribute to how a person perceives risk.
The World of Dickens
On one end of the traditional risk spectrum is the stereotypical widow or orphan. Not the ones with the enormous trust funds, but those from the world of Charles Dickens.
This group has very little money to begin with so preservation of capital is paramount. They invest in the hope of generating enough positive cash flow to buy their daily gruel. If you ask them about risk, they will say anything that could possibly reduce their original capital is risky.
The widow would definitely not want to double down at the blackjack table. She would also be uncomfortable investing in common stocks, corporate bonds, or real estate; investments with any uncertainty in repayment of the original capital.
This investor is only interested in guaranteed investments where her money is secure.
Versus the Wolves of Wall Street
On the other end of the risk spectrum is the hot shot young Wall Street finance expert.
If you ask about risk, you will get a long convoluted response that probably makes little, if any, sense. One involving the Greek alphabet (Alpha, Beta), strange acronyms (CAPM, SML), fun mathematical expressions (normal distributions, variability of returns, standard deviations), and crazy men (Sharpe, Treynor).
Like the lyrics from a pop song, the phrase “variability of returns” would endlessly echo in your head.
At the end of the explanation, you would probably back slowly from the room, grab a stiff drink, and return to the widows and orphans. At least they made some sense.
While the concept of investment risk is unique to each person, may I suggest that the average investor take a view somewhere in between Dickensian widows and Wolf of Wall Street financial experts. Closer to the expert’s view of the world would be my recommendation, but each person must be comfortable with their own risk profile. If not, there will be many sleepless nights filled with angst and Pepto-Bismol for your growing ulcer.
Investment Risk Defined
In looking at risk from the middle of the spectrum, investment risk is simply the probability that the actual return on an investment will be different than the expected return.
The greater the probability that the returns will differ, the greater the risk. The greater the certainty that the expected result will actually transpire, the lesser the risk. This is where the phrase “variability of returns” arises and we will look at it in detail later.
Sounds complicated. But when we get through our discussion of risk and returns, you will see it is not that bad.
A Simple Example
Let us use a simple example. If you invest $975.90 in a 6 month, 5% US T-Bill you will receive $1000.00 at maturity. The US government issues and guarantees payment on T-Bills. Unless you believe that the US government will default on their debts you are certain to receive the full amount.
In terms of the above definition, the probability that the actual return of capital ($1000.00) will be different than the expected return ($1000.00) is zero. The actual and expected returns ($24.10) are identical. You know the actual outcome with 100% certainty.
You expect to receive $1000. You actually receive exactly what you expected. Zero risk as actual equals expected.
For this reason the interest rate offered on short term US T-Bills is commonly considered the risk-free rate of return. There is no risk that the expected and actual returns will be different. The investment itself is considered to be risk-free.
Note this assumes that governments pay their debts. This assumption keeps eroding over time.
What about a common share of ABC Inc? The current share price is $9.76. Professional analysts agree, on average, that the price should increase to $11 at the end of 6 months. By investing $975.90 into ABC and not US T-Bills, you expect to receive $1100.00 after 6 months. An improvement from the $1000.00 you would receive from the T-Bill investment.
You invest your money into ABC shares, then promptly fly to Peru to spend the 6 months studying Incan civilization in the Andes. Far from wi-fi or cell phone connectivity. But thinking about that extra profit you are earning.
At the end of the 6 months you return home and go to sell the shares, fully expecting to enjoy that extra $100 in profit. Imagine your surprise when you find that the share price is now trading at $9.00 and you have actually lost money on the transaction. In this case the expected return ($1100.00) was significantly different than the actual return ($900.00). That is the impact of investment risk.
You expect to receive $1100. You actually receive a different amount than you expected. The fact that you did not receive exactly as expected represents the riskiness of the investment.
Note that it has nothing to do with receiving less ($900) than you expected ($1100) or initially invested ($976). Had you received $1500, it is still different than what you expected, so still represents risk.
The investment risk is simply the difference between what you expected to receive versus what you actually received.
Note that the higher the investment risk (measured by standard deviation), the greater chance the actual return will differ from the expected in higher levels. Hence the use of the term “volatility” for investment risk. Greater the risk, the more volatile the asset. The less risk, the more stable the expected returns will be over time.
This is also quite a real example. If any of you have ever invested in a stock based on analysts’ recommendations and/or price estimates, you will understand the percentage time they hit the mark. Seldom if ever.
We will review the relationship between risk and return in detail as it is critical to understanding the investment process.
For today though, I ask you to think about the following scenario.
How Do You View Investment Risk?
You have $1000.00 to invest and two options are available. Unless stated otherwise, we will always ignore costs in simple examples (e.g. transaction costs, taxes, management fees). Something never to ignore in real life.
You can invest in a 1 year US Government Bond yielding 5%. At the end of the term you will receive $1050.00 with 100% certainty.
Or you can invest in ABC, trading at $10 per share. Expert consensus is that the share price will rise to $10.50 in 1 year. This will provide the same expected 5% return as with the US Government Bond.
But ABC is not the US government. Also, other factors may be at play that impact the certainty of the price forecasts. The probability of actually receiving the expected return is less than 100%. You may receive more, you may receive less. It is impossible to predict with certainty.
Which would you choose for your investment? Many investors would choose the more certain return. Especially given that the expected returns are identical.
Investing 101
That tends to be an investment axiom.
If two investments offer identical expected returns, investors normally choose the lower risk asset. Conversely, if two investments offer the same level of risk, then investors will choose the asset with the higher expected return.
Investor Specific Risk Tolerance
But what if the experts’ consensus on ABC increased to $12 per share in a year? Does the higher potential return make up for the greater risk of ABC versus the US bond?
If not, how about a consensus price of $14 in one year? Or perhaps $16? What about if the consensus is only $8?
At what price point does the higher risk of ABC versus the risk-free bond make it a worthwhile gamble/investment?
What if there was no average consensus? Rather, there is a 25% probability the stock falls to $8, a 25% probability that it rises to $16, and a 50% probability that it rises to $12?
Does this new scenario change your investment decision?
How you answer these questions helps define your individual risk tolerance.
As for the “correct” answer, that is unique to the investor. And the level of investment risk assigned to ABC.
We will consider these examples when we get to the risk-return discussion.
Next up though, the two components of investment risk and factors that influence them.

